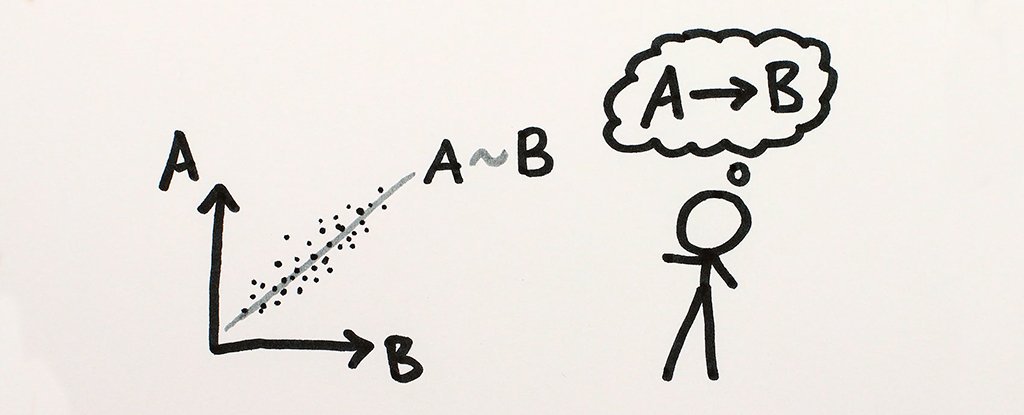
Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir. İki değişken arasındaki ilişki miktarı, ikili ya da basit korelasyon denen korelasyon teknikleriyle hesaplanır. Bir değişkenin iki ya da daha çok değişken ile olan ilişkisi çoklu korelasyon; bu değişkenlerden birinin sabitlenerek diğer değişkenler ile olan ilişkisi ise kısmi korelasyon teknikleriyle hesaplanır. Örneğin;
Öğrencilerin okul öncesi eğitime başlama yaşları (ay olarak) ile birinci sınıf başarısı arasındaki ilişki.
Öğrencilerin istatistik başarı puanları ile istatistiğe yönelik tutumları arasındaki ilişki.
Değişkenler arasındaki ilişki, korelasyon katsayısı ile hesaplanmaktadır.
Hangi korelasyon katsayısının kullanılacağı;
- Değişkenlerin hangi ölçek düzeyinde ölçüldüğüne
- Değişkenlerin sürekli veya süreksiz olmalarına
- Verilerin doğrusal olup olmamasına göre değişmektedir.
Basit (İkili) Korelasyon
Bir bireye ait iki ölçüm olduğunda bu iki değişken arasındaki ilişkiyi belirler. Korelasyon analizi sonucunda, doğrusal ilişki olup olmadığı ve varsa bu ilişkinin derecesi korelasyon katsayısı ile hesaplanır. Korelasyon katsayısı “r” ile gösterilir ve -1 ile +1 arasında değerler alır.

İlişkilerin Yorumu
1. Pearson Momentler Çarpımı Korelasyon Katsayısı (r)
En az eşit aralıklı ölçek düzeyinde ölçülen iki sürekli değişken arasındaki doğrusal ilişkinin derecesinin belirlenmesinde kullanılır.
A ve B değişkenleri arasında manidar bir ilişki var mıdır? sorusunun cevabı aranır.
Pearson Momentler Çarpımı Korelasyon Katsayısının Yorumu
Korelasyon katsayısı -1 ile +1 arasında değerler alır.
- r= -1 ise tam negatif doğrusal bir ilişki vardır.
- r= +1 ise tam pozitif doğrusal bir ilişki vardır.
- r= 0 ise iki değişken arasında ilişki yoktur.
Pearson Momentler Çarpımı Korelasyon Katsayısının Yorumu

Açıklanan Varyans
Değişkenlerden birindeki değişimin ne kadarının diğer değişken tarafından açıklandığının yüzde olarak ifade edilebilmesini sağlar.
Değişkenlerin birbirlerinde açıkladıkları varyans miktarı korelasyon katsayının karesine eşittir ve buna determinasyon katsayısı denir.
Örneğin Türkçe başarısı ile okuma hızı arasındaki korelasyon r=0.80 olsun. Buna göre determinasyon katsayısı r2 = 0.64’dür
Buna göre, öğrencilerin okuma hızındaki toplam değişkenliğin %64’ü Türkçe dersindeki başarılarından kaynaklanmaktadır. Ya da öğrencilerin Türkçe dersindeki başarılarının %64’ü okuma hızlarındaki değişimden kaynaklanmaktadır; biçiminde yorumlanabilir. Ayrıca geriye kalan %36’lık varyansın da başka değişkenlerden kaynaklandığı söylenebilir.
2. Spearman Brown Sıra Farkları Korelasyon Katsayısı (rho, rs)
Sıralı puanlar kullanılarak ölçülen iki değişken arasındaki doğrusal ilişkiyi açıklar.
Eşit aralıklı ya da eşit oran düzeyindeki ölçümler sıralı ölçeğe dönüştürülerek analiz edilmesi gerektiğinde de ölçümler sıralı ölçeğe dönüştürülerek uygulanabilir.
Ayrıca Pearson korelasyonundaki değişkenler, normal dağılım varsayımını sağlamadığında da Pearson korelasyon yerine kullanılır.
3. Nokta Çift Serili Korelasyon Katsayısı
Biri sürekli (en az aralık ölçeğinde), diğeri iki kategorili gerçek süreksiz (cinsiyet gibi) bir değişken arasındaki doğrusal ilişkiyi açıklamak için kullanılır.
4. Çift Serili Korelasyon Katsayısı
Sürekli bir değişken ile gerçekte sürekli ancak yapay olarak iki kategorili (yaşı iki kategoriye ayırmak gibi) süreksiz duruma getirilen bir değişken arasındaki ilişkinin hesaplanmasında kullanılır.
5. Dörtlü Korelasyon Katsayısı
Sınıflama ölçeğinde ölçülmüş iki kategorili iki süreksiz değişken [sosyoekonomik düzey (düşük-yüksek) ile cinsiyet gibi) arasındaki ilişkinin ölçülmesinde kullanılır.
Regresyon Analizi
Regresyon, bir değişkene ilişkin ölçümlerin grup ortalamasına doğru çekilmesidir.
Regresyon analizi, aralarında ilişki olan iki ya da daha fazla değişkenden birinin bağımlı değişken, diğerlerinin bağımsız değişkenler olarak ayrımı ile aralarındaki ilişkinin matematiksel bir eşitlik ile açıklanması sürecidir.
Bağımsız Değişken: Genellikle x ile gösterilir. Başka bir değişken tarafından etkilenmeyen ama y’nin nedeni olan ya da onu etkilediği düşünülen (açıklayıcı) değişkendir.
Bağımlı Değişken: Genellikle y ile gösterilir. x değişkenine bağlı olarak değişebilen ya da ondan etkilenen (açıklanan) değişkendir.
Regresyon denklemi;

Kaynak: https://acikders.ankara.edu.tr (Tıkla)